Standard form of a circle:

(x-h)² + (y-k)² = r²
where point (h,k) is the center, and r is radius
This can be expanded to x² + y² + Dx + Ey + F = 0  (aka the General form)
Can go from general form to standard form by completing the square

Ellipse - sum of distance from two foci is a constant

points on the ellipse follow the formula:
  (x-h)²/a² + (y-k)²/b² = 1
and
   c² = a² - b²
center C = (h,k)
a = distance from C to long end of ellipse (along major axis)
b = distance from C to close end of ellipse (along minor axis)
c = distance from center to a focus
(x,y) = a point on the ellipse

Any point on a parabola is equidistant from the focus and the directrix

vertex of a parabola in quadratic form: for y = ax^2 + bx + c, then x = -b/2a

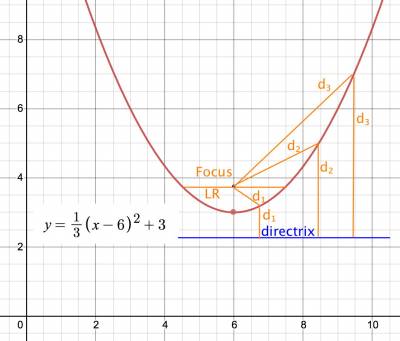
standard form of a parabola:

(x-h)² = 4p(y-k)  => if p>0, opens up, p<0 opens down
(y-k)² = 4p(x-h)  => if p>0, opens to right, p<0 opens to left  
where point (h,k) is the vertex, and 
 p (sometimes called a instead) = minimum distance between 
    parabola and vertex (is on axis of symmetry, which is 
    perpendicular to the directrix)
this can be rewritten as:
  y = (1/4p)(x-h)² + k for an up/down parabola
  x = (1/4p)(y-k)² + h for a left/right parabola
LR (latus rectum line) is line parallel to directrix going 
    thru focus (if you know focus, easy to find LR points 
    and vertex, then draw the function). Length of LR is |4p|

Hyperbola - difference of distance from two foci is a constant

If there are foci F and G, point P then distances |PF - PG| = C

Opens left/right:

(x-h)²/a² - (y-k)²/b² = 1 
   center at (h, k)
   vertices //a// units left/right of center
   asymptotes pass through center with slope ± b/a.

Opens up/down:

(y-k)²/b² - (x-h)²/a² = 1 
    center at (h, k)
    vertices //b// units up/down of center
    asymptotes pass through center with slope ± b/a.

Back to geometry, algebra/pre-calc or math page.