Table of Contents

Trigonometry

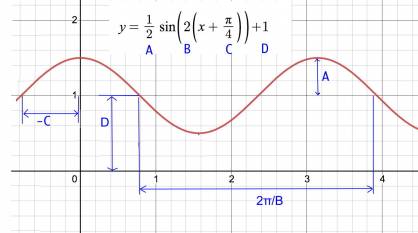
transformations of sine or cosine function: y = a * sin(b(x - c)) + d

Sine Wave Transformations

(Graphics from www.Desmos.com, labeling was added) a = amplitude, c = phase shift, d = vertical shift, 2π/b = period (for tan the period is π/b)

Sin/Cos table

Radians Degrees Cos Sin
0 0 1 0
π/6 30 √3/2 1/2
π/4 45 √2/2 √2/2
π/3 60 1/2 √3/2
π/2 90 0 1
2π/3 120 -1/2 √3/2
3π/4 135 -√2/2 √2/2
5π/6 150 -√3/2 1/2
π 180 -1 0
-5π/6, 7π/6 210 -√3/2 -1/2
-3π/4, 5π/4 225 -√2/2 -√2/2
-2π/3, 4π/3 240 -1/2 -√3/2
-π/2, 3π/2 270 0 -1
-π/3, 5π/3 300 1/2 -√3/2
-π/4, 7π/4 315 √2/2 -√2/2
-π/6, 11π/6 330 √3/2 -1/2
0, 2π 360 1 0

Conversion Theorems

double angle: 2θ 

sin(2θ) = 2sin(θ)cos(θ)
cos(2θ) = cos²(θ) - sin²(θ)
        = 2*cos²(θ) - 1
        = 1 - 2*sin²(θ)

negative angles: 

sin(-θ) = -sin(θ)
cos(-θ) = cos(θ)
tan(-θ) = -tan(θ)

additive, subtractive: 

sin(a+b) = sin(a)cos(b) + cos(a)sin(b)
cos(a+b) = cos(a)cos(b) - sin(a)sin(b)
sin(a-b) = sin(a)cos(b) - cos(a)sin(b)
cos(a-b) = cos(a)cos(b) + sin(a)sin(b)

complements: 

sin(θ) = cos(π/2 - θ)
cos(θ) = sin(π/2 - θ)

See also

Back to math page.