User Tools
urp:graphing
Graphing curves and circles
Circles
Standard form of a circle:
(x-h)² + (y-k)² = r² where point (h,k) is the center, and r is radius This can be expanded to x² + y² + Dx + Ey + F = 0 (aka the General form) Can go from general form to standard form by completing the square
Ellipse
Ellipse - sum of distance from two foci is a constant
points on the ellipse follow the formula: (x-h)²/a² + (y-k)²/b² = 1 and c² = a² - b² center C = (h,k) a = distance from C to long end of ellipse (along major axis) b = distance from C to close end of ellipse (along minor axis) c = distance from center to a focus (x,y) = a point on the ellipse
Parabolas
Any point on a parabola is equidistant from the focus and the directrix
vertex of a parabola in quadratic form: for y = ax^2 + bx + c, then x = -b/2a
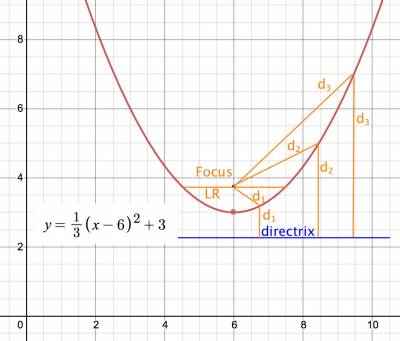
standard form of a parabola:
(x-h)² = 4p(y-k) => if p>0, opens up, p<0 opens down
(y-k)² = 4p(x-h) => if p>0, opens to right, p<0 opens to left
where point (h,k) is the vertex, and
p (sometimes called a instead) = minimum distance between
parabola and vertex (is on axis of symmetry, which is
perpendicular to the directrix)
this can be rewritten as:
y = (1/4p)(x-h)² + k for an up/down parabola
x = (1/4p)(y-k)² + h for a left/right parabola
LR (latus rectum line) is line parallel to directrix going
thru focus (if you know focus, easy to find LR points
and vertex, then draw the function). Length of LR is |4p|
Hyperbola
Hyperbola - difference of distance from two foci is a constant
If there are foci F and G, point P then distances |PF - PG| = C
Opens left/right:
(x-h)²/a² - (y-k)²/b² = 1 center at (h, k) vertices //a// units left/right of center asymptotes pass through center with slope ± b/a.
Opens up/down:
(y-k)²/b² - (x-h)²/a² = 1
center at (h, k)
vertices //b// units up/down of center
asymptotes pass through center with slope ± b/a.
Back to geometry, algebra/pre-calc or math page.
urp/graphing.txt · Last modified: 2021-10-21 by nerf_herder

